Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
Tags
- Selenium
- openCV
- 선그래프
- queue
- 백준
- 가상환경
- 파이썬
- dataframe
- 알고리즘
- 정보처리기사 c언어
- 코딩테스트
- MySQL
- programmers
- 노마드코딩
- NumPy
- String Method
- type hint
- 알고리즘스터디
- aws jupyter notebook
- 자료구조
- Matplotlib
- python
- javascript
- pandas
- Join
- Stack
- Algorithm
- 프로그래머스
- 알고리즘 스터디
- 데이터시각화
Archives
- Today
- Total
조금씩 꾸준히 완성을 향해
[Sklearn] 선형 회귀(Linear Regression), 다항 회귀(Polynoimal Regression), 규제(Ridge, Lasso) 본문
AI/Machine Learning
[Sklearn] 선형 회귀(Linear Regression), 다항 회귀(Polynoimal Regression), 규제(Ridge, Lasso)
all_sound 2022. 10. 28. 00:11선형 회귀 (Linear Regression)
# 농어의 길이, 무게 확인
import matplotlib.pyplot as plt
plt.scatter(perch_length, perch_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

# 훈련, 테스트 세트 나누기
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
perch_length, perch_weight, random_state=42)
# 1차원 배열 => 2차원 배열
train_input = train_input.reshape(-1, 1)
test_input = test_input.reshape(-1, 1)# 모델 적용
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_input, train_target)
# 50cm 농어의 무게 예측
print(lr.predict([[50]]))
# [1241.83860323]
# 기울기, 절편
print(lr.coef_, lr.intercept_)
# [39.01714496] -709.0186449535477
주요 파라미터
- fit_intercept : 절편을 학습 여부 선택 (디폴트는 True)
- normalize : 매개변수 무시 여부 (디폴트는 False)
- copy_X : X의 복사 여부
- n_jobs : 계산에 사용할 작업 수
내장 속성
- coef_ : 기울기, 종종 계수(coefficient), 가중치(weight) 출력
- intercept_ : 절편값 출력
# 회귀선 그래프로 확인
# 훈련 세트의 산점도
plt.scatter(train_input, train_target)
# 15에서 50까지 회귀선 그래프
plt.plot([15, 50], [15 * lr.coef_ + lr.intercept_, 50 * lr.coef_ + lr.intercept_])
# 50cm 농어 데이터
plt.scatter(50, 1241.8, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
# 훈련 세트와 테스트 세트의 결정 계수(R²) 확인
print(lr.score(train_input, train_target))
print(lr.score(test_input, test_target))
# 훈련 세트 0.939846333997604
# 테스트 세트 0.8247503123313558
다항회귀 (polynoimal regression)
# 데이터 준비
import pandas as pd
df = pd.read_csv('http://bit.ly/perch_csv')
perch_full = df.to_numpy()
# train, test 분리
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(perch_full, perch_weight, random_state=42)
- 다항 특성 만들기
# 회귀식 차수 늘리기
from sklearn.preprocessing import PolynomialFeatures
# degre=2
poly = PolynomialFeatures()
poly.fit([[2,3]])
# 1(bias), 2, 3, 2**2, 2*3, 3**2
print(poly.transform([[2,3]]))
# [[1. 2. 3. 4. 6. 9.]]※ PolynomialFeatures 은 변환기 ( fit => 학습이 아니라 새로운 특성을 만들어주는 역할)
- 회귀 모델에 적용
# train 세트 변환
poly = PolynomialFeatures(include_bias=False) #절편 특성 빼기 #default는 2차항
poly.fit(train_input)
train_poly = poly.transform(train_input)
print(train_poly.shape) # (42, 9)poly.get_feature_names()
# ['x0', 'x1', 'x2', 'x0^2', 'x0 x1', 'x0 x2', 'x1^2', 'x1 x2', 'x2^2']# test 세트 변환
test_poly = poly.transform(test_input)# 선형회귀 모델에 적용
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))
# 0.9903183436982124
# 0.9714559911594134# 더 많은 특성 만들기
poly = PolynomialFeatures(degree=5, include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)
print(train_poly.shape) #(42, 55)lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))
# 0.9999999999991097
# -144.40579242684848 => 과대적합
규제 (Regularization)
- 표준화
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(train_poly)
train_scaled = sc.transform(train_poly)
test_scaled = sc.transform(test_poly)
▶ Ridge 회귀 (L2 규제)
from sklearn.linear_model import Ridge
ridge = Ridge()
ridge.fit(train_scaled, train_target)
print(ridge.score(train_scaled, train_target))
print(ridge.score(test_scaled, test_target))
# 0.9896101671037343
# 0.9790693977615391# 적절한 규제 강도 찾기
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
train_score = []
test_score = []
for alpha in alpha_list:
ridge = Ridge(alpha=alpha)
ridge.fit(train_scaled, train_target)
train_score.append(ridge.score(train_scaled, train_target))
test_score.append(ridge.score(test_scaled, test_target))
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show()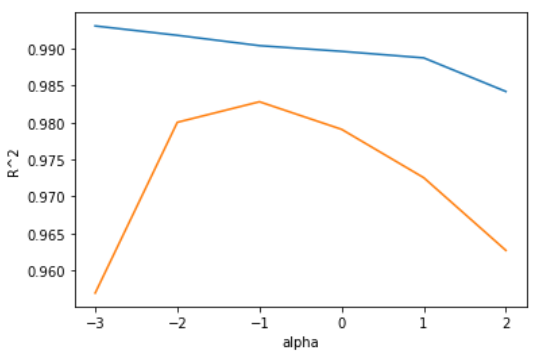
ridge = Ridge(alpha=0.1)
ridge.fit(train_scaled, train_target)
print(ridge.score(train_scaled, train_target))
print(ridge.score(test_scaled, test_target))
# 0.9903815817570365
# 0.9827976465386884
▶ Lasso 회귀 (L1 규제)
from sklearn.linear_model import Lasso
lasso = Lasso()
lasso.fit(train_scaled, train_target)
print(lasso.score(train_scaled, train_target))
print(lasso.score(test_scaled, test_target))
# 0.989789897208096
# 0.9800593698421883# 적절한 규제 강도 찾기
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
train_score = []
test_score = []
for alpha in alpha_list:
lasso = Lasso(alpha=alpha)
lasso.fit(train_scaled, train_target)
train_score.append(lasso.score(train_scaled, train_target))
test_score.append(lasso.score(test_scaled, test_target))
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show()
ridge = Ridge(alpha=10)
ridge.fit(train_scaled, train_target)
print(ridge.score(train_scaled, train_target))
print(ridge.score(test_scaled, test_target))
# 0.988728468997471
# 0.9725329582461567print(np.sum(lasso.coef_ == 0)) #52
- 참고 - [한빛미디어] 혼자 공부하는 머신러닝+딥러닝, 박해선 저
'AI > Machine Learning' 카테고리의 다른 글
| [Sklearn] 로지스틱 회귀(Logistic Regression) (0) | 2022.10.29 |
|---|---|
| [Sklearn] K-Nearest Neighbor Regression(k-최근접 이웃 회귀) (1) | 2022.10.27 |
| [Sklearn] K-Nearest Neighbor(k-최근접 이웃 분류)와 표준화(Scaling) (0) | 2022.10.27 |



