| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Selenium
- Stack
- pandas
- aws jupyter notebook
- python
- programmers
- type hint
- 코딩테스트
- 알고리즘스터디
- 자료구조
- Matplotlib
- 가상환경
- javascript
- String Method
- dataframe
- openCV
- 데이터시각화
- 알고리즘 스터디
- 파이썬
- 노마드코딩
- MySQL
- 백준
- 선그래프
- 프로그래머스
- NumPy
- queue
- 정보처리기사 c언어
- Join
- 알고리즘
- Algorithm
- Today
- Total
조금씩 꾸준히 완성을 향해
[Algorithm] 기초 문제 / 소수(에라토스테네스 체) 본문
▶ 문제
자연수 N이 입력되면 1부터 N까지의 소수의 개수를 출력하는 프로그램을 작성하세요. 만약 20이 입력되면 1부터 20까지의 소수는 2, 3, 5, 7, 11, 13, 17, 19로 총 8개입니다. 제한시간은 1초입니다.
▶ 입력 설명
첫 줄에 자연수의 개수 N(2<=N<=200,000)이 주어집니다.
▶ 출력 설명
첫 줄에 소수의 개수를 출력합니다.
▶ 입력
20
▶ 출력
8
▷ 내가 짜본 코드
import sys
sys.stdin=open("input.txt", "r")
n = int(input())
a = []
for i in range(2, n+1):
for j in range(2, n+1):
if i % j == 0:
if j != i :
break
else :
a.append(i)
print(len(a))
'에라토스테네스의 체'가 무엇인지 몰랐기 때문에 최대한 내 머리에서 끄집어 낼 수 있는 논리로 코드를 작성했다.
반복문을 두 번이나 돌려서 소수인지 아닌지 일일히 확인한다는 게 진짜 쉬운 일은 아니었다.
메모장에 예시를 써가며 한참을 고민한 결과 그래도 작동하는 코드를 만들 수 있었다.
첫번째 for문은 input값까지의 숫자를 하나하나 가져오는 과정이고
두번째 for문은 그 수가 소수인지 아닌지 확인하는 과정이다.
소수는 1과 자기 자신으로만 나누어 지는 수이다.
그래서 일단 나누어지는 모든 수의 범위를 잡고
if i % j == 0:
자기자신이 아닌 수로 나누어지는 수를 만났을 때는 반복문을 멈추었고,
if j != i :
break
자기자신으로 나누어 지는 수만 배열에다 추가를 하였다.
else :
a.append(i)
그렇게 소수를 모두 넣은 배열을 만들 수 있었고, 그 배열의 길이를 구하면 소수의 개수가 출력된다.
▷ 예시 코드
import sys
sys.stdin=open("input.txt", "r")
n=int(input())
ch=[0]*(n+1)
cnt=0
for i in range(2, n+1):
if ch[i]==0:
cnt+=1
for j in range(i, n+1, i):
ch[j]=1
print(cnt)
'에라토스테네스의 체'라는 개념을 이용하면 훨씬 더 간단하게 소수의 개수를 구할 수 있다.
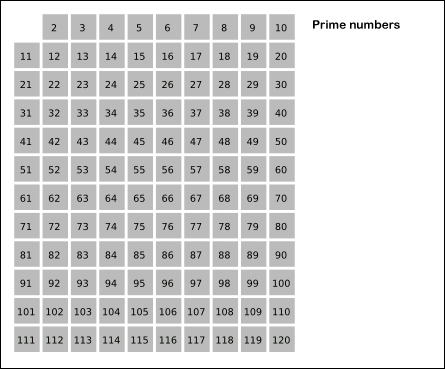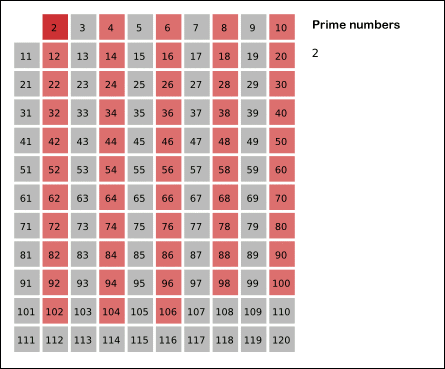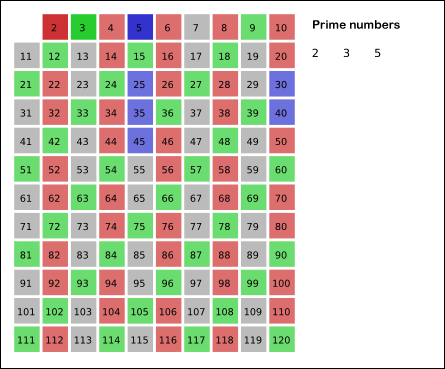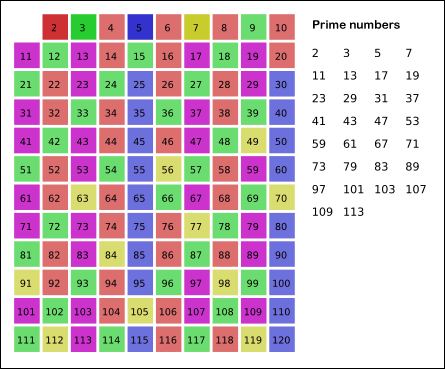
(출처: 위치백과)
먼저 2부터 시작해 원하는 숫자까지를 나열한다.
2는 소수임으로 체크하고 2의 배수를 모두 지운다.
3도 소수임으로 체크하고 3의 배수를 모두 지운다.
그 다음으로 등장하는 수인 5도 소수임으로 체크하고 5의 배수를 모두 지운다.
이 과정을 반복하면 원하는 구간 안의 모든 소수가 남는다.
이 논리를 코드로 구현하기 위해서는 먼저 이런 list를 만들어야 한다.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | n |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 |
ch=[0]*(n+1)index에는 확인할 숫자가 차례로 들어가고, 값은 우선 모두 0으로 세팅한다.
시작 index인 2부터 for문을 돌아 값이 0인지 확인이 되면 counting을 한다. (이후로 값이 0이면 소수로 취급한다.)
cnt=0
for i in range(2, n+1):
if ch[i]==0:
cnt+=1
그리고 이중 for문을 돌려 모든 2의 배수에 1을 할당한다.
for j in range(i, n+1, i):
ch[j]=1
그 후 다시 상위 for문으로 돌아가 다음 살아남은 수인 3이 0인지 확인하고 맞으면 카운팅하고 3의 배수를 1로 셋팅한다. 당연히 확인하는 숫자의 값이 1이면 카운팅을 하지 않게 된다. 이 과정을 n까지 반복하면, 소수의 개수가 cnt에 모두 담긴다.
이 문제도 그냥 반복해서 익숙해지는 수밖에 없는 것 같다.
에라토스테네스의 체가 중학교 교육과정에 있다는데 전혀 생각이 안나서 좀 슬펐다.
수학 좀 열심히 해놓을껄 후회가 되는 순간...ㅠㅠ
'DataStructure & Algorithm > 문제풀이' 카테고리의 다른 글
| [Algorithm] 기초 문제 / 점수 계산 (0) | 2022.09.05 |
|---|---|
| [Algorithm] 기초 문제 / 뒤집은 소수 (0) | 2022.09.05 |
| [Algorithm] 기초 문제 / 자릿수의 합 (0) | 2022.08.29 |
| [Algorithm] 기초 문제 / K번째 큰 수 (0) | 2022.08.27 |
| [Algorithm] 기초 문제 / K번째 수 (0) | 2022.08.27 |
